Элементы аналитической геометрии

Для того чтобы уметь синтезировать изображения на экране компьютера необходимо предложить способ математического описания объектов в трехмерном пространстве или на плоскости. Окружающий нас мир с точки зрения практических приложений описывают как трехмерное евклидово пространство. Под описанием трехмерного объекта будем понимать знание о положении каждой точки объекта в пространстве в любой момент времени. Положение точек в пространстве удобно описывается с помощью декартовой системы координат.

Для того чтобы ввести декартову систему координат проведем три направленные прямые линии, не лежащие в одной плоскости, которые называются осями, в трехмерном пространстве так чтобы они пересекались в одной точке – начале координат. Выберем на этих осях единицу измерения. Тогда положение любой точки в пространстве будем описывать через координаты этой точки, которые представляют собой расстояния от начала координат до проекций точки на соответствующие оси координат. Проекцией точки на координатную ось называется точка пересечения плоскости, проходящей через заданную точку и параллельной плоскости, образованной двумя другими осями координат. Например, на рис. 1 проекцией точки

 на ось  является точка , которая принадлежит плоскости, параллельной плоскости .

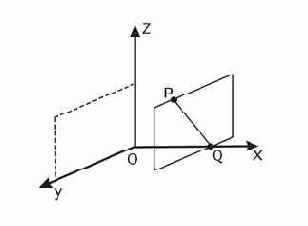
Рис. 1. Нахождение координаты

 точки P.

В общем случае оси системы координат могут располагаться под произвольными, хотя и фиксированными углами друг относительно друга. Для практических расчетов гораздо удобнее когда эти оси расположены взаимно перпендикулярно. Такая система координат называется ортогональной. В ортогональной системе координат проекцией точки

 на ось является единственная точка на оси такая, что отрезок прямой, проведенной из этой точки к точке  является перпендикулярным к данной оси.

Таким образом, положение в пространстве точки

 описывается ее координатами, что записывается как . Взаимное расположение осей в ортогональной системе координат в трехмерном пространстве может быть двух видов. Проведем ось  слева направо, а ось  снизу вверх, как показано на рис. 2.

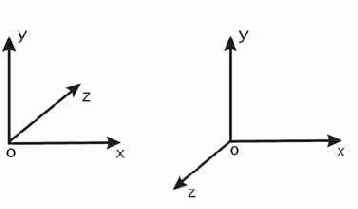
Рис.2. Левосторонняя и правосторонняя системы координат.

Ось   при этом может проходить как в направлении от наблюдателя в плоскость листа, так и от плоскости листа к наблюдателю. В первом случае система координат будет называться левой или левосторонней, а во втором случае – правой или правосторонней. Более точное определение правой и левой систем координат можно дать следующее. Если посмотреть из положительной полуоси  в направлении начала координат, то для совмещения положительной полуоси  с положительной полуосью  необходимо повернуть  относительно начала координат против часовой стрелки – в этом случае имеем правую систему координат; если же поворот производится по часовой стрелке – то система координат левая*. Существует также легкий способ определения вида системы координат по правой или левой руке, как показано на рис. 3. Для левой руки большой, указательный и средний пальцы формируют левую тройку ортогональных векторов. То же относится и к их циклическим перестановкам.



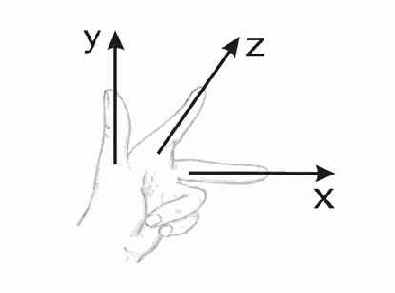
Рис. 3. Определение левосторонней системы координат по левой руке.

Декартовы координаты точек позволяют описывать статичное положение объектов в пространстве. Однако для проведения каких-либо действий над объектами необходимо иметь дополнительные математические конструкции. В качестве одной из таких конструкций применяют радиус-векторы. Радиус-векторы обладают всеми свойствами векторов, но имеют одну особенность: начало радиус-вектора находится всегда в начале координат, а конец радиус-вектора лежит в некоторой точке пространства. Это свойство радиус-векторов позволяет поставить во взаимно однозначное соответствие всем точкам пространства соответствующие им радиус-векторы. Формально это соответствие запишем в следующем виде. Пусть точка  имеет координаты , то есть , и  – радиус-вектор, конец которого находится в точке , где  – тройка единичных базисных векторов, или просто нормированный базис. Тогда точке  взаимно однозначно соответствует радиус-вектор , или . Таким образом, можно легко переходить от координат точек к радиус-векторам и обратно.





  Далее мы увидим что представление радиус-вектора в виде линейной комбинации векторов базиса имеет вполне конкретное практическое применение. Отметим, что радиус-вектор иногда определяют как преобразование переноса точки из начала координат в заданную точку пространства с известными координатами. При этом умножение радиус-вектора  на число  означает перенос точки из начала координат в направлении вектора  на расстояние , где прямые скобки означают операцию взятия модуля вектора:



Сложение радиус-векторов  можно рассматривать как перенос точки  по направлению вектора  на расстояние .

Рассмотрим теперь каким образом можно использовать координаты точек и радиус-векторы для описания прямых и плоскостей в трехмерном пространстве. Под описанием прямой понимаем знание того принадлежит ли точка с заданными координатами нашей прямой или нет. То есть нужно получить некую математическую зависимость или уравнение прямой. Мы получим уравнение прямой двумя способами.

Во-первых, известно, что две различные точки определяют в пространстве прямую. Выберем в пространстве две точки  и  и проведем через них прямую, как показано на рис 4.



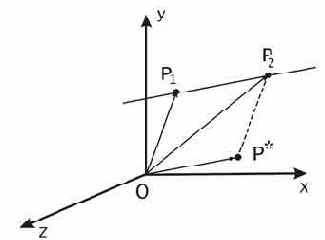
Рис. 4. Вывод уравнения прямой в трехмерном пространстве.

Проведем от точки  к точке  вектор . Тогда радиус-вектор , определяющий некоторую точку на прямой, можно получить сложением, например, вектора  и вектора , умноженного на некоторое число . Или . Фактически мы уже получили уравнение прямой, но не через координаты двух точек на прямой, а другим способом, с помощью, так называемых, базового радиус-вектора  и направляющего радиус-вектора . Преобразуем это уравнение к виду в котором используются только координаты двух исходных векторов  и :

                (1)

Из этого векторного равенства получаем три равенства для соответствующих координат:



Попарно разделив эти уравнения друг на друга для того чтобы избавится от коэффициента , получаем следующую систему уравнений, определяющую нашу прямую в трехмерном пространстве:



                       (2)

В практических задачах иногда бывает нужно узнать лежит ли некоторая точка, принадлежащая прямой, внутри отрезка, заданного координатами своих концов на данной прямой, или снаружи. Для решения этой задачи перепишем уравнение (1) в следующем виде:

                                       (3)

При  получаем точки прямой, лежащие между  и . При  – точки лежащие на прямой за , при  – точки, лежащие на прямой за . Для проверки этого просто подставьте в уравнение вместо  значения 0 и 1.

Перейдем теперь к выводу уравнения плоскости. Мы сможем получить его тремя путями. Но прежде напомним определение скалярного произведения. Для двух радиус-векторов  и  скалярным произведением назовем число , где  - угол между векторами  и . Для векторов запись вида  или  также будем считать скалярным произведением. Скалярное произведение можно выразить через координаты векторов:

 ,

так как при раскрытии скобок скалярные произведения перпендикулярных векторов базиса по определению обращаются в ноль.

Используем свойства скалярного произведения для вывода уравнения плоскости. Рассмотрим некоторую плоскость в пространстве и некоторую точку , про которую мы знаем, что она лежит в этой плоскости, как показано на рисунке 5.



Рис. 5. Вывод уравнения плоскости в трехмерном пространстве.

 Возьмем также некоторый радиус-вектор , перпендикулярный нашей плоскости. Этот вектор назовем нормалью к плоскости. Пусть теперь требуется определить принадлежит ли некоторая точка (или радиус-вектор)  плоскости или нет. Для этого заметим, что для любой точки , принадлежащей плоскости, вектор  и радиус-вектор нормали  – перпендикулярны. А это значит, что их скалярное произведение равно нулю:

                                             (4)

Так мы уже получили уравнение плоскости. Раскроем скобки и запишем его в более удобном виде: , где константа . Если , а , то в координатной записи наше уравнение плоскости запишется в виде



                                       (5)

Известно что плоскость может быть задана тремя точками, лишь бы они не лежали на одной прямой, то есть если они не коллинеарны. Получим уравнение плоскости для трех заданных точек. Для этого рассмотрим определение векторного произведения. Результатом векторного произведения двух векторов  является вектор , модуль которого равен , и направлен он перпендикулярно плоскости в которой лежат векторы  и , причем векторы

 – образуют правую тройку векторов (см. определение правой системы координат), здесь  также угол между векторами  и . Для векторов единичного базиса, образующих правую тройку, как следует из определения: , , . Векторное произведение также  подчиняется дистрибутивному закону как и скалярное произведение. Однако векторное произведение не коммутативно, а именно, если для векторов , то , что также прямо следует из определения. Координаты векторного произведения легко получить разложив векторы, участвующие в произведении, по базису, а затем раскрыв скобки, подобно тому как это уже было проделано для скалярного произведения. Есть и другой, неформальный, но легче запоминаемый способ получения координат векторного произведения, с помощью разложения следующего определителя по его первой строке. Если  и , тогда



Сведем теперь условия в новой постановке задачи нахождения уравнения плоскости к предыдущему случаю, где мы использовали вектор нормали. Пусть заданы фиксированные векторы  и , не лежащие на одной прямой, определяющие плоскость, уравнение которой требуется получить (рис. 6).



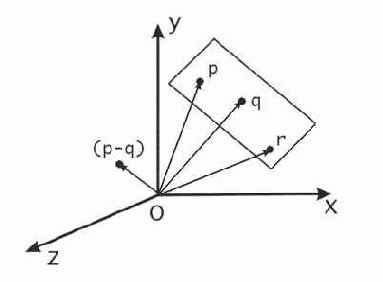
Рис. 6. Вывод уравнения плоскости проходящей через три точки.

Результат векторного произведения любых двух неколлинеарных векторов, параллельных нашей плоскости, будет вектором перпендикулярным плоскости. И как раз такими являются векторы разности  и . Выберем их векторное произведение в качестве вектора нормали, то есть . Тогда, если  – произвольный радиус-вектор, принадлежащий плоскости, то искомым уравнением плоскости будет, аналогично формуле (4):



,

причем в последней скобке вместо вектора  можно было использовать, например, векторы  или . Не будем далее расписывать это уравнение через координаты, так как это не трудно проделать самостоятельно.

Рассмотрим еще несколько определений и типичных задач, решение которых не должно вызывать замешательств.

Иногда бывает необходимо вычислить длину проекции радиус-вектора не на ось системы координат, а на другой радиус-вектор. Найдем длину проекции вектора  на вектор . Эта ситуация изображена на рис.7, из которого, очевидно, следует и решение задачи.



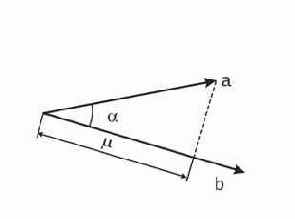
Рис. 7. Проекция вектора  на вектор .

Искомая длина проекции: ==.

Как видно, если длина вектора, на который проецируется другой вектор, равна единице, то длина проекции будет просто равна скалярному произведению этих векторов.

С помощью формулы длины проекции вектора на вектор можно еще одним способом получить уравнение плоскости, если заметить, что длины проекций радиус-векторов, принадлежащих плоскости, на вектор нормали к плоскости всегда равны между собой.

Решим задачу нахождения минимального расстояния от начала координат до плоскости. Очевидно, что это расстояние необходимо откладывать вдоль прямой, определяемой вектором нормали к плоскости. Но для нахождения этого расстояния надо найти сначала точку пересечения прямой с плоскостью. Поэтому решим в общем виде задачу нахождения точки пересечения прямой и плоскости. Пусть искомая точка, или соответствующий радиус-вектор называется x. Тогда эта точка должна одновременно удовлетворять уравнениям прямой и плоскости, например,  и . Подставив x из первого уравнения во второе, найдем значение константы , которое затем подставим в исходное уравнение прямой для получения координат искомой точки:

   

Уравнение прямой вдоль вектора нормали к плоскости запишем как . Перед тем как подставить в это уравнение выражение для , заметим, что для нашей прямой, базовый вектор  равен нулю, а направляющий вектор совпадает с вектором нормали  .


Учитывая это, запишем:



Отсюда искомое расстояние от начала координат до плоскости равно

                                                       



В том случае когда вектор нормали  является нормированным, константа  в уравнении плоскости равна расстоянию от начала координат до данной плоскости.

Кроме определения положения точек в пространстве радиус-векторы также определяют некоторое направление в пространстве.

Направление, определяемое радиус-вектором, удобно описывать с помощью, так называемых, направляющих косинусов. Пусть радиус-вектор  составляет с осями координат ,  и  углы, соответственно,  и  (рисунок 8). Тогда его направляющими косинусами будут:

, ,



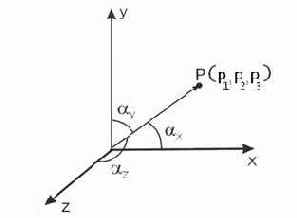
Рис. 8. Направляющие косинусы.

Отсюда, очевидно, вытекают следующие свойства направляющих косинусов:

.

Направляющие косинусы пропорциональны соответствующим координатам:

 ,

а в случае, когда вектор  нормирован, значения его координат равны соответствующим направляющим косинусам.

Рассмотрим далее функциональное представление плоскости. Для этого в уравнении (5) перенесем константу из правой части в левую и запишем функцию трех переменных .

Если подставить координаты точки, принадлежащей данной плоскости в это уравнение, то . Если же точка не принадлежит плоскости, то значение функции, очевидно, будет больше или меньше нуля. Интересен тот факт, что для точек, лежащих по одну и ту же сторону от плоскости функция  имеет всегда один и тот же знак. С помощью чертежа на рисунке 9 , легко показать, что для точек лежащих в полупространстве, порождаемом плоскостью и содержащем начало координат, функция  отрицательна, а для точек лежащих в другом полупространстве, как, например, для точки  на рисунке, она положительна. В общем же случае необходимо учитывать направление вектора нормали.



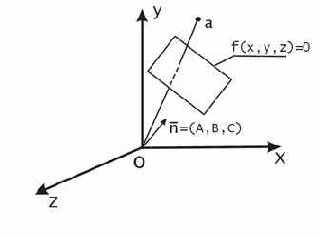
Рис. 9. Функциональное представление плоскости.

Свойство сохранения знака функции  удобно использовать в алгоритмах удаления невидимых ребер и граней для определения того лежат ли точки по одну сторону от плоской грани или нет.


Для этого достаточно лишь подставить значения координат точек в функциональное представление плоскости, определяемой соответствующей гранью и проверить совпадают знаки функции или нет. Аналогичные рассуждения можно проделать и для более простого случая прямой на плоскости. Тогда для любой точки на плоскости можно определить ее нахождение в одной их полуплоскостей на которые прямая делит плоскость. Это свойство используется в следующем примере.

Рассмотрим далее три метода решения классической задачи определения принадлежности точки внутренней или граничной области треугольника. Эта задача имеет, конечно же, много решений, некоторые из которых может придумать и сам читатель. Пусть на плоскости  заданы три точки  и , образующие треугольник (рис. 10).



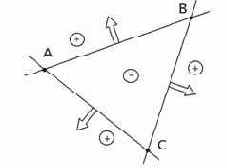
Рис. 10. Внутренняя область треугольника соответствует отрицательным направлениям векторов нормалей.

Через каждую пару вершин треугольника можно провести прямую. Замкнутая область пересечения трех полуплоскостей, образованных этими прямыми есть внутренняя область треугольника. Пользуясь вектором нормали  можно записать уравнение прямой на плоскости: . Идея первого метода состоит в том, чтобы записать функциональные представления уравнений прямых, образующих стороны треугольника, таким образом, чтобы внутренняя область треугольника соответствовала, например, отрицательным значениям. Тогда условием принадлежности внутренней области треугольника будут отрицательные значения трех функциональных уравнений прямых при подстановке координат проверяемой точки. Основной проблемой в этом методе является правильный выбор направления вектора нормали к прямой.

Следующий метод основан на преобразовании треугольника с помощью операции переноса таким образом чтобы проверяемая точка совпала с началом координат. Поворотом плоскости вокруг начала координат расположим одну (любую) из вершин треугольника на оси . Тогда если знаки координат  оставшихся двух точек совпадают, то искомая точка лежит вне треугольника.


Если же знаки различны, то берем следующую из оставшихся вершин треугольника и поворотом плоскости устанавливаем ее на ось . После чего вновь проверяем знаки координат  двух других вершин, и т.д.

      

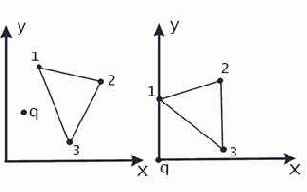
                                      Рис. 11. Точка  вне треугольника.

Условием принадлежности точки внутренней области треугольника будет несовпадение знаков  ? координат оставшихся двух вершин после каждого из трех поворотов.



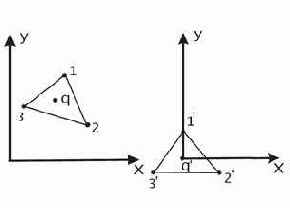
Рис. 12.Точка  внутри треугольника.

 Нахождение точки на одной из сторон треугольника легко определяется по несовпадению знаков -координат двух вершин которые после одного из поворотов оказались лежащими на оси . Этот метод эффективен когда больше вероятность что точка лежит вне треугольника. Отрицательной его чертой является необходимость вычисления синусов и косинусов углов при повороте системы координат.

Третий из приводимых здесь методов представляется наиболее компактным и скоростным с вычислительной точки зрения. Этот метод был предложен автору Д. Чистяковым в 1999 году. Заметим, что очень просто можно определить принадлежность точки внутренней области треугольника – единичного симплекса, то есть треугольника, образованного точками с координатами , , . Для этого достаточно чтобы координаты искомой точки имели значения в отрезке  и выполнялось условие , где  и  ? координаты точки. Заметим также, что с помощью аффинных преобразований на плоскости или непрерывных деформаций любой треугольник можно преобразовать к единичному симплексу.



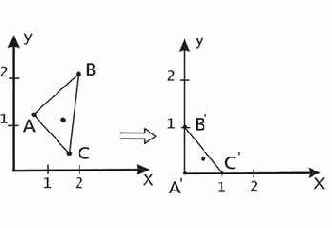
Рис. 13. Приведение произвольного треугольника к единичному симплексу.

 После таких преобразований внутренняя и внешняя области треугольника остаются таковыми. Применив такое преобразование к искомой точке, достаточно затем будет определить ее нахождение во внутренней или внешней области симплекса. Найдем такое преобразование. Координаты векторов единичного базиса совпадают с координатами точек  и  симплекса, соответственно. Будем считать что точка  треугольника совпадает с началом координат.


Этого всегда можно добиться параллельным переносом треугольника на вектор . При этом координаты точек  и  треугольника суть коэффициенты разложения соответствующих векторов  и  по единичному базису. Матрица перехода от единичного базиса к базису на векторах  и  составлена из координат этих векторов.



 Значит для обратного перехода к единичному базису, (на векторах которого построен симплекс), необходимо найти обратную матрицу:

 .

Умножение радиус-вектора искомой точки на матрицу  дает  точку которую достаточно проверить на попадание во внутреннюю или внешнюю область единичного симплекса, как было указано выше.


Содержание раздела

---