Кубические сплайны

Рассмотрим задачу проведения гладких кривых по заданным граничным точкам, или задачу интерполяции. Поскольку через две точки можно провести сколь угодно много гладких кривых, то для решения этой задачи необходимо ограничить класс функций, которые будут определять искомую кривую. Математическими сплайнами называют функции, используемые для аппроксимации кривых. Важным их свойством является простота вычислений. На практике часто используют сплайны вида полиномов третьей степени. С их помощью довольно удобно проводить кривые, которые интуитивно соответствуют человеческому субъективному понятию гладкости. Термин “сплайн” происходит от английского spline – что означает гибкую полоску стали, которую применяли чертежники для проведения плавных кривых, например, для построения обводов кораблей или самолетов.

Рассмотрим в начале сплайновую функцию для построения графика функции одной переменной. Пусть на плоскости задана последовательность точек

, причем

. Определим искомую функцию

, причем поставим два условия:

Функция должна проходить через все заданные точки:

2) Функция должна быть дважды непрерывно дифференцируема, то есть иметь непрерывную вторую производную на всем отрезке

На каждом из отрезков

будем искать нашу функцию в виде полинома третьей степени:

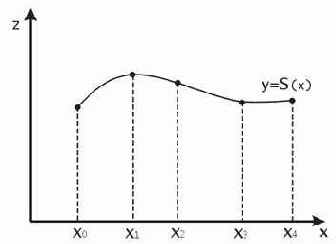
Рис. 40. Сплайновая функция.

Задача построения полинома сводится к нахождению коэффициентов

. Поскольку для каждого из отрезков

необходимо найти 4 коэффициента

, то всего количество искомых коэффициентов будет

. Для нахождения всех коэффициентов определим соответствующее количество уравнений. Первые

уравнений получаем из условий совпадения значений функции во внутренних узлах

. Следующие

уравнений получаем аналогично из условий совпадения значений первых и вторых производных во внутренних узлах. Вместе с первым условием получаем

уравнений. Недостающие два уравнения можно получить заданием значений первых производных в концевых точках отрезка

. Так могут быть заданы граничные условия.

Перейдем к более сложному случаю – заданию кривых в трехмерном пространстве. В случае функционального задания кривой

возможны многозначности в случае самопересечений и неудобства при значениях производных равных

. Ввиду этого будем искать функцию в параметрическом виде. Пусть

- независимый параметр, такой что

. Кубическим параметрическим сплайном назовем следующую систему уравнений:

Координаты точек на кривой описываются вектором

, а три производные задают координаты соответствующего касательного вектора в точке. Например, для координаты

.

Одним из способов задания параметрического кубического сплайна является указание координат начальной и конечной точек, а также векторов касательных в них. Такой способ задания называется формой Эрмита. Обозначим концевые точки

, а касательные векторы в них

. Индексы выбраны таким образом с учетом дальнейшего изложения.

Будем решать задачу нахождения четверки коэффициентов

, так как для оставшихся двух уравнений коэффициенты находятся аналогично. Запишем условие для построения сплайна:

(*)

Перепишем выражение для

в векторном виде:

.

Обозначим вектор строку

и вектор столбец коэффициентов

, тогда

.

Из (*) следует, что

. Для касательных

. Отсюда получаем векторно-матричное уравнение:

.

Эта система решается относительно

нахождением обратной матрицы размером

.

Здесь

- эрмитова матрица,

- геометрический вектор Эрмита. Подставим выражение

для нахождения

. Аналогично для остальных координат:

.

Выпишем в явном виде формулы для вычисления координат точек сплайна. Так как

, то умножая справа на

, получаем:

.

Четыре функции в скобках называются функциями сопряжения.

Форму кривой, заданной в форме Эрмита, легко изменять если учитывать, что направление вектора касательной задает начальное направление, а модуль вектора касательной задает степень вытянутости кривой в направлении этого вектора, как показано на рис. 41.

Рис. 41. Параметрический сплайн в форме Эрмита.

Вытянутость кривой вправо обеспечивается тем, что

.

Рассмотрим форму Безье, которая отличается от формы Эрмита способом задания граничных условий, а именно, вместо векторов

вводятся точки (и соответствующие им радиус векторы)

, как показано на рис.42, такие что выполняются условия:

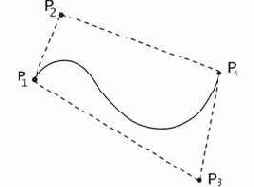
Рис. 42. Параметрический сплайн в форме Безье.

Переход от формы Эрмита к форме Безье осуществляется преобразованием:

, (*)

где

- геометрический вектор Безье. Подставляя это в выражение для

, получаем

.

Полезным свойством сплайнов в форме Безье является то что кривая всегда лежит внутри выпуклой оболочки, образованной четырехугольником

. Это свойство можно доказать, пользуясь тем, что в выражении (*) коэффициенты принимают значения от 0 до 1 и их сумма равна единице.

Заметим, что матрица вида

- называется матрицей Безье.

Содержание раздела